fitting module
- lys.fitting.addFittingFunction(func, name)[source]
Add fitting function to the lys fitting module.
Use
lys.functions.registerFittingFunction()instead of this function.
List of pre-defined fitting functions
- lys.fitting.Functions.cos(x, position, height, frequency, phase)[source]
Cosine function
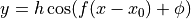
- Parameters:
position –
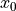 .
.height –
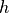 .
.frequency –
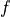 .
.phase –
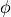 .
.
- lys.fitting.Functions.doubleExp(x, position, height, a, b)[source]
Double exponential function with step.
![y = h\theta (x-x_0)(1-\exp[-(x-x_0)/a]^2)\exp[-(x-x_0)/b]](../_images/math/9d5e0de7101e8fc0893bdecc34b2818417e8ceb9.png)
- Parameters:
position –
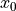 .
.height –
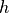 .
.a –
 .
.b –
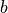 .
.
- lys.fitting.Functions.error(x, position, height, fwhm)[source]
Error function for fitting.
For convenience, this function is defined as
![h(\mathrm{erf}[(x-x_0)/\tau] + 1)/2](../_images/math/e5832cf762acbba9297bae9cc28c5517cc0977d5.png)
erf is error function (scipy.special.erf).
FWHM is of gaussian function integrated.
- Parameters:
position –
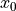 .
.height –
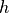 .
.fwhm – :
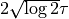 .
.
- lys.fitting.Functions.exp(x, position, height, a)[source]
Simple exponential function
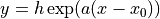
- Parameters:
position –
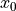 .
.height –
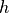 .
.a –
 .
.
- lys.fitting.Functions.gauss(x, position, height, sigma)[source]
Simple gaussian
![y=h\exp[-(x-x_0)^2/2\sigma^2]](../_images/math/fd1a2102327de19bf8978356f57ad2118c4b099f.png)
- Parameters:
position –
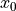 .
.height –
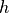 .
.sigma –
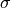 .
.
- lys.fitting.Functions.lorentz(x, position, height, fwhm)[source]
Lorentz function.
![y = hd^2/[(x-x_0)^2+d^2]](../_images/math/fd6b689ac7fe3524fb67e09f792ca28805062da2.png)
- Parameters:
position –
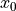 .
.height –
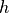 .
.fwhm –
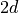 .
.
- lys.fitting.Functions.relaxOsci(x, position, height, frequency, phase, offset, tau)[source]
Relaxed ocillation.
![y=h(C + cos[f(x-x_0)+\phi])\exp[-(x-x_0)/\tau]\theta(x-x_0)](../_images/math/a44c48a89cea4e23cbbfcd70376d1dbde9f8cc68.png)
- Parameters:
position –
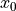 .
.height –
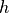 .
.frequency –
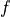 .
.phase –
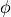 .
.offset –
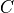 .
.tau –
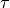 .
.
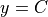
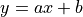
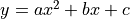
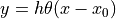
![y = h\theta(x-x_0)\exp[-a(x-x_0)]](../_images/math/1599be59972a4ce7604d4ed987eec7c2b17aedb7.png)